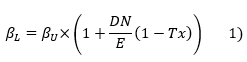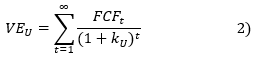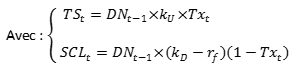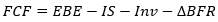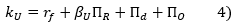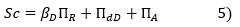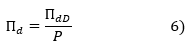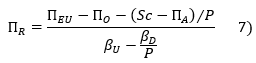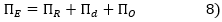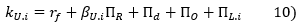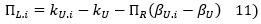L'approche « Adjusted Present Value » ou APV consiste à tenir compte de l'effet de levier d'endettement, non pas en corrigeant le taux d'actualisation, mais en ajustant les flux.
Parmi les multiples formalisations existantes de l'APV, nous retenons celle qui nous semble être la seule cohérente avec le modèle le plus répandu d'estimation de l'effet de levier sur le risque systématique, i.e. le modèle d'Hamada.
Il est équivalent d'actualiser au coût des fonds propres avec levier un cash flow libre pour l'actionnaire ou d'actualiser au coût des fonds propres à dette nulle un cash flow à dette nulle ajusté du bouclier fiscal et du coût systématique du levier.
La prime de risque MEDAF se déduit de l'écart entre le TRI à endettement nul du marché et le taux sans risque, après prise en compte du biais optimiste, du spread de crédit, du bêta de la dette et du taux de récupération.
Connaissant le coût du capital à dette nulle du marché et celui des quantiles de taille parmi lesquels nous répartissons les sociétés de notre échantillon, il devient possible de déterminer la prime de taille par différence, après ajustement de l'écart de risque systématique entre le quantile et le marché.